北リポ

今日の方程式。
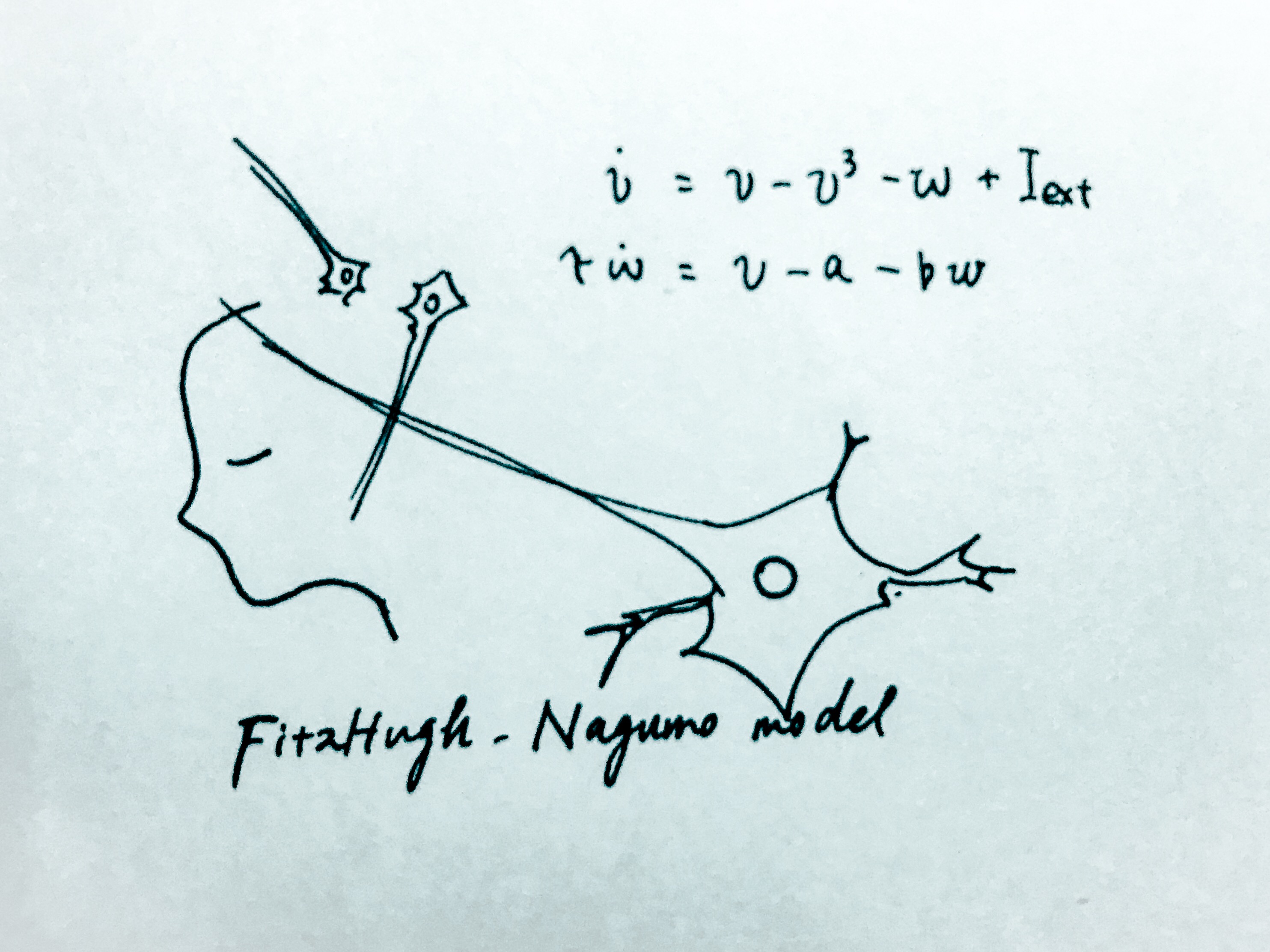
神経細胞のふるまいを再現する、
フィッツヒュー・南雲モデル。

ホジキン・ハクスリーモデルという
モデルをかんたんにしたもので、
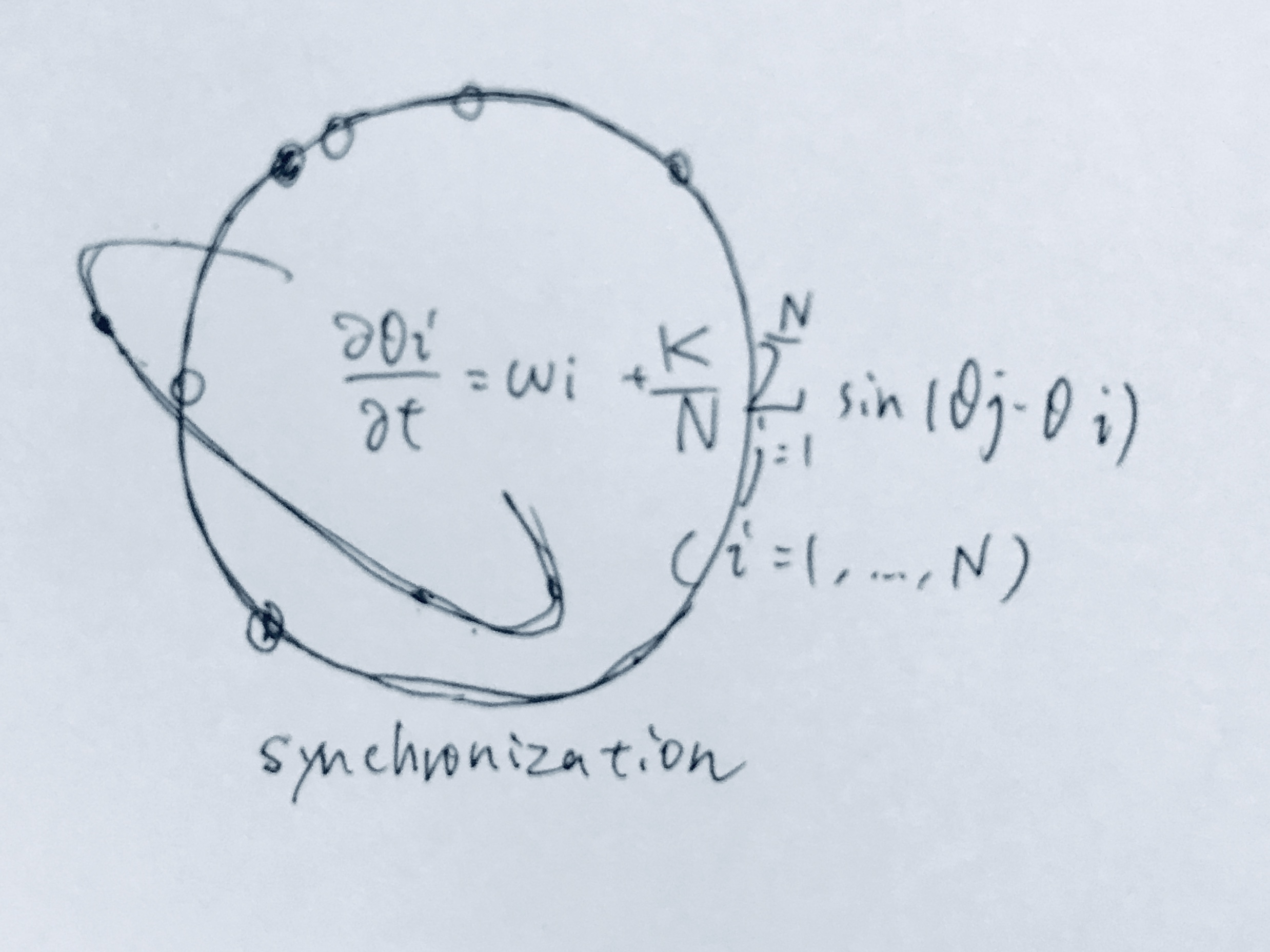
生物リズムを表す代表的な方程式です。

この方程式の特殊な場合が、
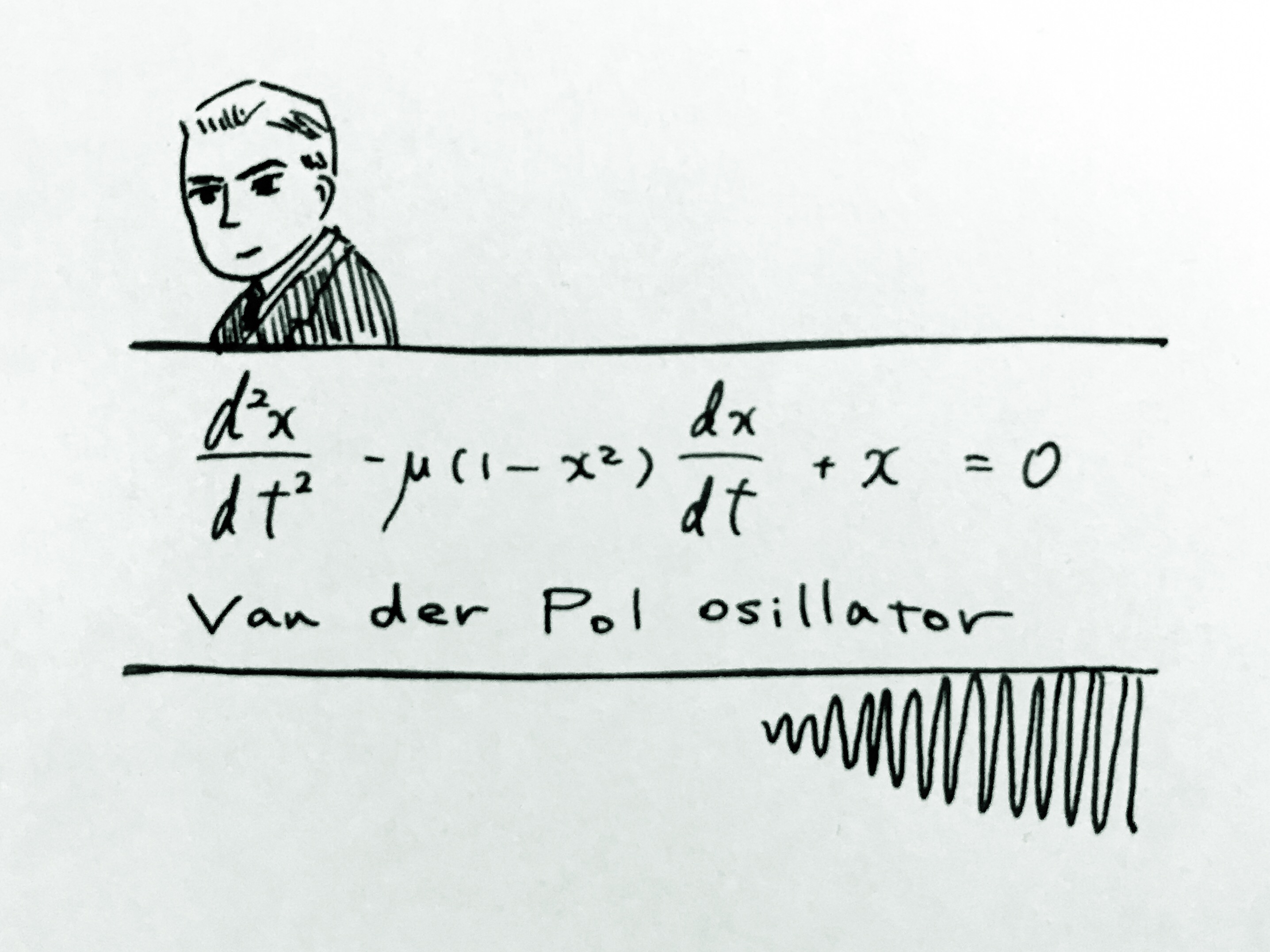
ファン・デル・ポール方程式。
こちらは真空管を用いた
電気回路についての研究から生まれました。

見た目には異なる現象も、
数理モデルにすることで
現象の核となる部分が取り出され、
同じ核をもつ現象とつながっていきます。

こういうところも、
物理学のおいしいところというか、
おもしろいところだと思います。

はやくも今年も10月が
終わってしまいました…

後期がはじまって、
卒研を本格的に
考え始めておりました。

半ばには力学系の会に参加しに
京都へひとり旅。

ゼミの進捗に毎週泣きながら
日を送っていた気がします…

社会人になっていてもいい年。
衣食住を満足させて、
仕事をはやく計画的にできるよう、
習慣をつくっていきたいです。

（めっちゃ真面目なこと書いた。
こういう自分を見ると少し安心します。
…いかんいかん。）

2018.11.3　かきもち

今日の方程式。
理想気体の状態方程式。

高校で習ったとき、先生が
「pv=って言われたら、nRTって答えられなきゃ
理系選択とは言えませんね～」
言っていたのを思い出す。
今はジョークだったんやな…とか思う。

この式のえらいところは、
ボイルの法則とシャルルの法則という
2つの法則を1つにまとめてあるところ。

では「理想」でない空気だったら、
どうなるでしょうか。

こんばんは。かきもちです。

少し前になりましたが、
10月13日、14日に
学生力学系の会という
（平たく言うと）勉強会に
参加してきました！

場所は京都大学。
人生初、関西への単独旅行です。
（関西空港、めっちゃ広かった）

京大付近は、
空気がにやにやしていて
「あー、ここが森見登美彦の…」
と勝手に納得していました。

それはそうとこの会、
力学系という分野を研究する
修士・博士の先輩方が、
学部生向けにプレゼンする、
というもの。

それまで興味をもったことに
「力学系」という言葉が
何度も出てきていたので、

「とりあえず行ってみよう」

と行くことを決意したのでした。

～後編へつづく～

今日の方程式。

真空管の中のカオス、
ファン・デル・ポール振動子。

このモデルを提案したのは
電気工学者、物理学者の
ファン・デル・ポール氏。
1900年代前半、ドイツの
科学者です。

この方程式、
自励振動という運動を
示すモデルのひとつ。

自励振動とは、
外から物体に加わった力が
振動させるような力でなくても、
物体が振動させるような力に変えて
自ら振動してしまう現象のこと。

北リポでは、これを使って
お風呂場見られるお湯の波面を
説明しようとしたことがあります。
（できなかったけど…）

数理モデルは、
いろいろな現象と
つながっていますね。

×　osillator
○　oscillator

いつの間にやら5週目に突入。
相変わらず論文を読んだり
本を読んだりする毎日です。

最近は特に免疫系や
社会の中の秩序構造に
興味をひかれています。

というのも、この土日、
宮台真司の本を読んでいて
「数理社会学」というワードを
知ってしまったのです…

社会を数理モデルで、
定量的にとらえるという
手法とか思想とか、
もうあるのか…！

と感激しつつ、

物理学をきちんとやらねばだぞ、
安易な方だと思って
追いかけてはならん、と
ブレーキをかけています。

免疫学は、
最近親知らずを抜いたときに

「人間ってこんなに
身体が傷ついたり汚れたりしても
生きてられるの、すごいな…」

「それを維持してるのって
免疫系だよな」

という、これまたひとつの
秩序を守るものとして
興味をもった次第です。

もっといろいろ知りたい。
知りたいことが多すぎる。

ちなみに3週目の終わりに、
案の定〆切に追われて

「私はなにもできないいい
情けないいい」

とか泣きながら帰りました…
不審者やん…

いまは元気です！大丈夫！

今日の方程式。

捕食者ー被捕食者関係を記述する、
ロトカ・ヴォルテラの方程式。

食べられるほうの数が増えると、
食べる方の数が増え、

すると食べられるほうの数が減り、
食べるほうもご飯に困って減る…

その間に食べられるほうが回復し…

という、
食べるほうと食べられるほうの
数の増減を表しています。

ロトカさんとヴォルテラさんが、
二人ともべつべつに考案したモデルです。

いずれも1900年代はじめごろに
考案しています。

 

研究室では、論文を読んだりしております。
読んでいますとまあ必ず、

あれ、わかんないぞ。
という部分が出てくるわけですね。

そうしますと、文字を追うよりは
一度目を閉じて考えたりもします。

で、こう気づくと夢の国だったりね。
秋だからかな。

…いや、一年中か。

今日の方程式。

同期現象を記述する、蔵本モデル。
その最もかんたんな場合を表す
方程式です。

リズムをもつものが集まったとき、
それらが相互作用して
リズムが揃えていく様を
表すことができます。

たとえば、ホタルの光。
東南アジアでは、
ひとつの木にとまった蛍が
一斉に明滅するそうです。

たとえば、心臓の拍動。
一つ一つの細胞が
リズムを刻んでいて、
それらのリズムが揃って
全体として拍動しています。

私とあなたも、
相互作用でつながっているのかも。

今日の方程式。

ラグランジュの運動方程式。
オイラー・ラグランジュの方程式とも。

解析力学という分野の
中心となる方程式です。

解析力学は、
古典力学のあとに生まれた
新しいタイプの力学です。

この運動方程式を計算していくと、
あのニュートンの運動方程式に
一致します。