タグ: 今日の方程式

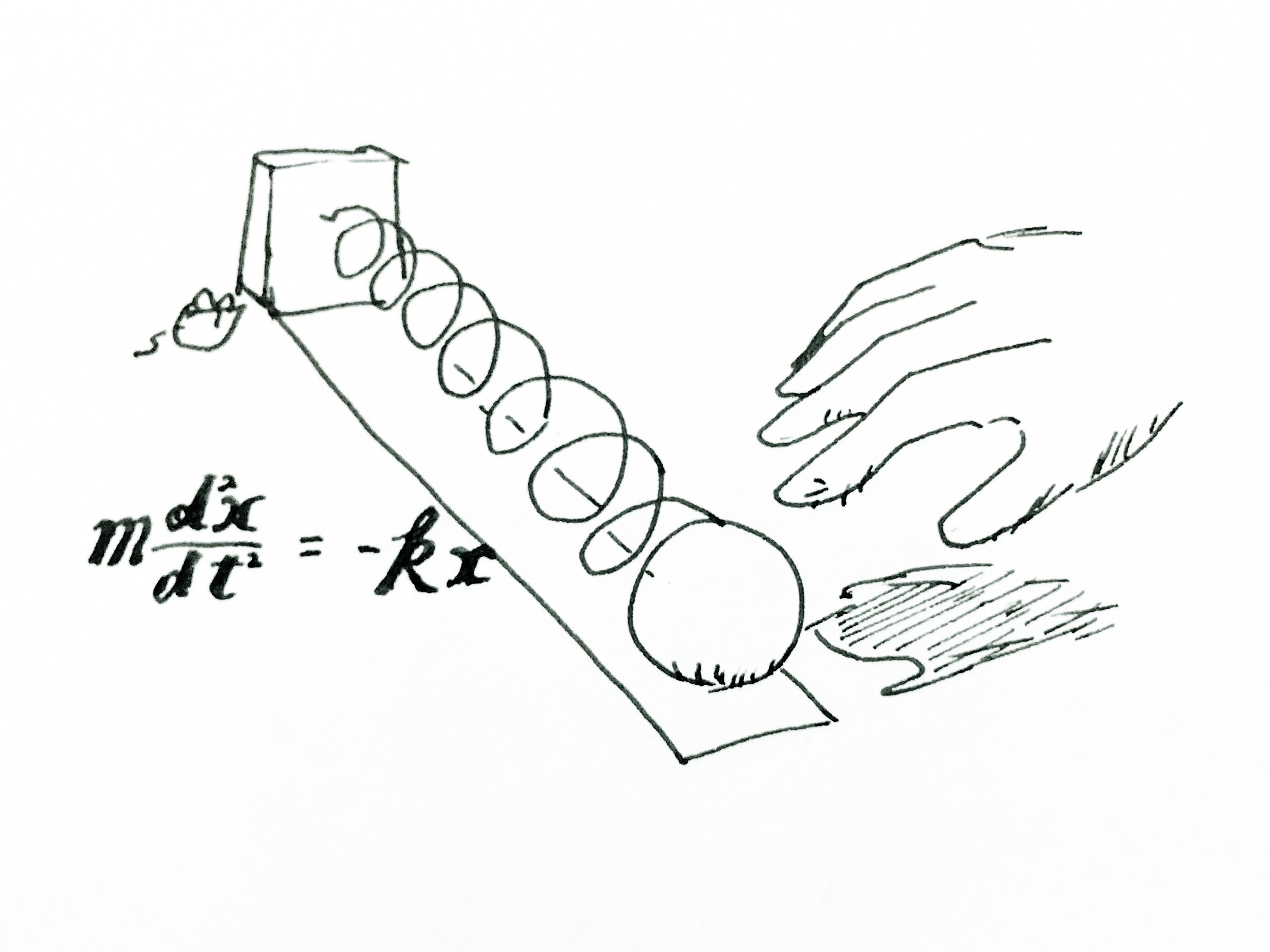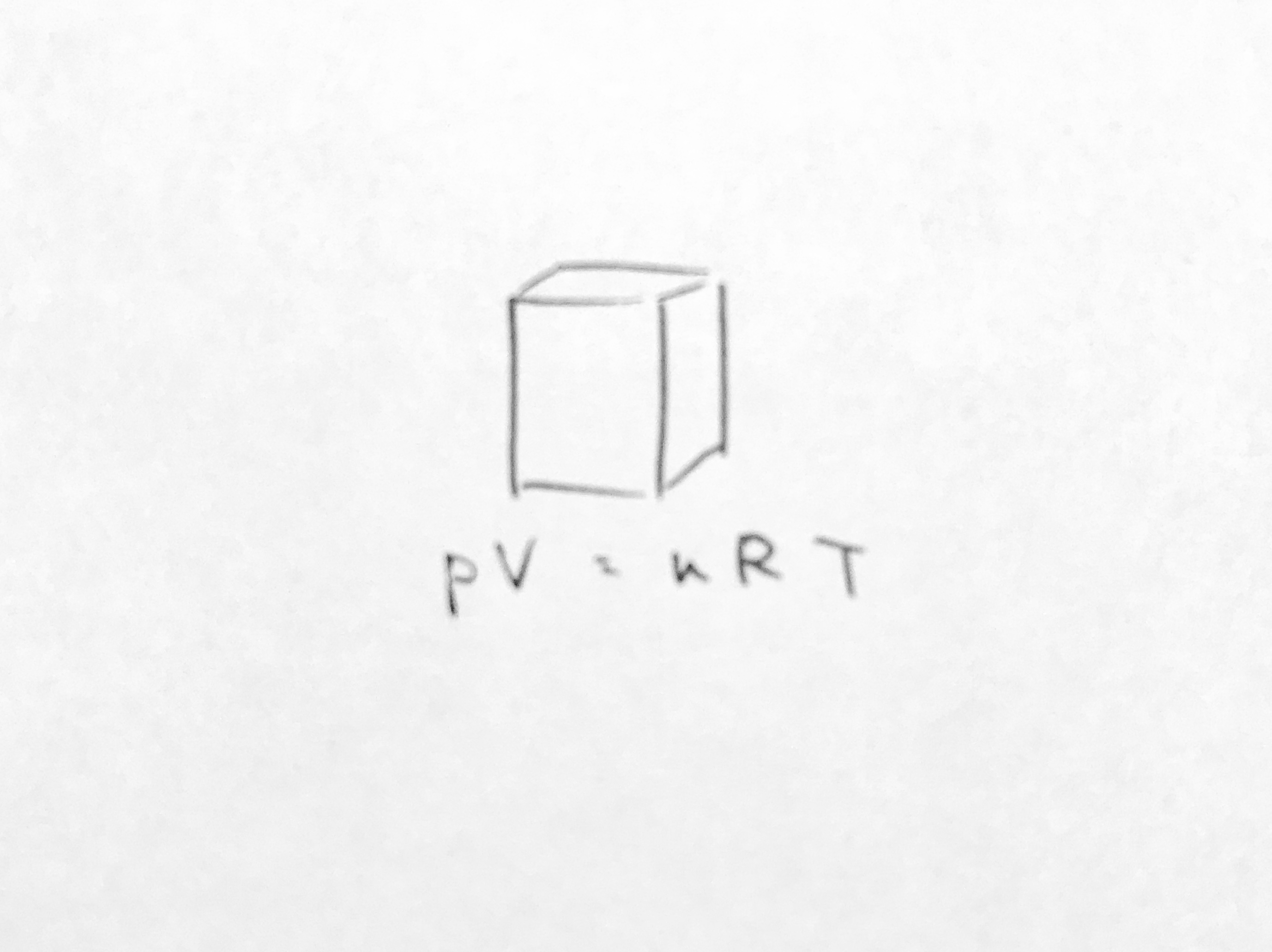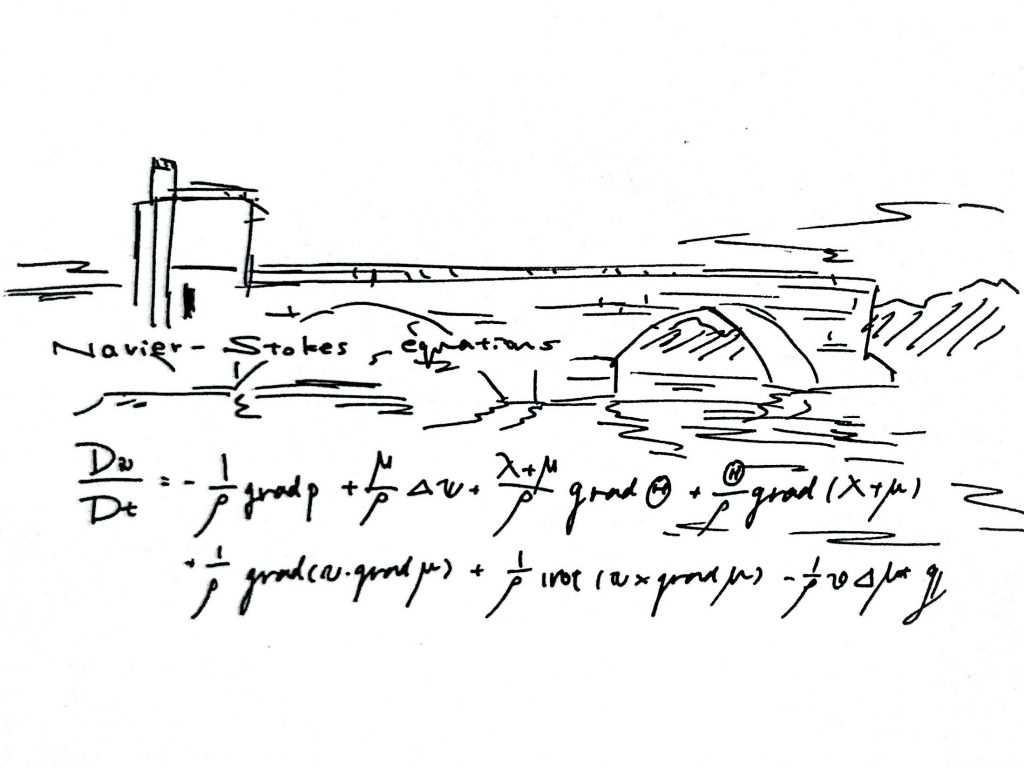
流体力学の基礎方程式。
基礎方程式とは、ニュートン力学でいう
運動方程式に当たるものです。

これを導いたのはアンリ・ナビエ。
19世紀フランスで活躍した、
技術者・科学者です。

この方程式、条件つきの場合を除いて
数学的な厳密解が見つかっていません。
解けるかどうかもわかっていないのです。
人類が流体を掴む日は来るのでしょうか…

REF:
パテント2013 知恵の輪 Vol.24
Wikipedia
予備校のノリで学ぶ ナビエ-ストークス方程式
ホーストン大学 Engines of Our Ingenuity
https://uh.edu/engines/epi2832.htm

最近、「今日の方程式」を
更新していて思う。

科学のことを正確に、
楽しく伝えるのって
難しい…。

勉強がまだ生焼けなので、
自分が思っている
おもしろポイントが
勘違いということがあるのだ。

“No.303「科学を伝える難しさ」” の続きを読む →

今日の方程式。
ジャパニーズ・アトラクタを示す
微分方程式。

カオスの先駆的な研究の一つです。

フックの法則に従わない
ばねの運動を再現します。

この方程式を満たすxとyは
カオス軌道を描きます。

これを発見したのは
当時京都大学大学院生だった、
上田睆亮（よしすけ）。
1961年のことでした。
当時はカオスという言葉もなく、
日本国内では注目されませんでした。

同じくカオスを示す
ローレンツ・アトラクタ―は
1963年の論文で報告されました。

その後上田の発見は1980年の
フランスの数理物理学者による論文で
日の目をみることとなります。

さらに上田は、この発見のまえに
1961年、カオス軌道を示すモデルを
すでに発見しています。

1960年代初めごろは、
世界でも同時多発的に
カオスが発見されていたのですね。

これはコンピューター技術の発展が
深く関わっていそうです。
うーん、どうしても長くなってしまう。
それはまた今度…。

今日の方程式。
水平ばね振り子の運動方程式。

高校で物理を履修したので、
黒板に書いてあったのを思い出します。

このとき小球は、
単振動という往復運動をします。

単振動は「調和振動」ともいい、
数理モデルの中で調和振動をするものを
「調和振動子」といいます。
英語でいうと、”harmonic oscilator”。
なんだかかっこいい。

今日の方程式。
神経細胞のふるまいを再現する、
フィッツヒュー・南雲モデル。

ホジキン・ハクスリーモデルという
モデルをかんたんにしたもので、
生物リズムを表す代表的な方程式です。

この方程式の特殊な場合が、
ファン・デル・ポール方程式。
こちらは真空管を用いた
電気回路についての研究から生まれました。

見た目には異なる現象も、
数理モデルにすることで
現象の核となる部分が取り出され、
同じ核をもつ現象とつながっていきます。

こういうところも、
物理学のおいしいところというか、
おもしろいところだと思います。

今日の方程式。
理想気体の状態方程式。

高校で習ったとき、先生が
「pv=って言われたら、nRTって答えられなきゃ
理系選択とは言えませんね～」
言っていたのを思い出す。
今はジョークだったんやな…とか思う。

この式のえらいところは、
ボイルの法則とシャルルの法則という
2つの法則を1つにまとめてあるところ。

では「理想」でない空気だったら、
どうなるでしょうか。

今日の方程式。

真空管の中のカオス、
ファン・デル・ポール振動子。

このモデルを提案したのは
電気工学者、物理学者の
ファン・デル・ポール氏。
1900年代前半、ドイツの
科学者です。

この方程式、
自励振動という運動を
示すモデルのひとつ。

自励振動とは、
外から物体に加わった力が
振動させるような力でなくても、
物体が振動させるような力に変えて
自ら振動してしまう現象のこと。

北リポでは、これを使って
お風呂場見られるお湯の波面を
説明しようとしたことがあります。
（できなかったけど…）

数理モデルは、
いろいろな現象と
つながっていますね。

×　osillator
○　oscillator

今日の方程式。

捕食者ー被捕食者関係を記述する、
ロトカ・ヴォルテラの方程式。

食べられるほうの数が増えると、
食べる方の数が増え、

すると食べられるほうの数が減り、
食べるほうもご飯に困って減る…

その間に食べられるほうが回復し…

という、
食べるほうと食べられるほうの
数の増減を表しています。

ロトカさんとヴォルテラさんが、
二人ともべつべつに考案したモデルです。

いずれも1900年代はじめごろに
考案しています。

 

今日の方程式。

同期現象を記述する、蔵本モデル。
その最もかんたんな場合を表す
方程式です。

リズムをもつものが集まったとき、
それらが相互作用して
リズムが揃えていく様を
表すことができます。

たとえば、ホタルの光。
東南アジアでは、
ひとつの木にとまった蛍が
一斉に明滅するそうです。

たとえば、心臓の拍動。
一つ一つの細胞が
リズムを刻んでいて、
それらのリズムが揃って
全体として拍動しています。

私とあなたも、
相互作用でつながっているのかも。

今日の方程式。

ラグランジュの運動方程式。
オイラー・ラグランジュの方程式とも。

解析力学という分野の
中心となる方程式です。

解析力学は、
古典力学のあとに生まれた
新しいタイプの力学です。

この運動方程式を計算していくと、
あのニュートンの運動方程式に
一致します。