タグ: 力学系

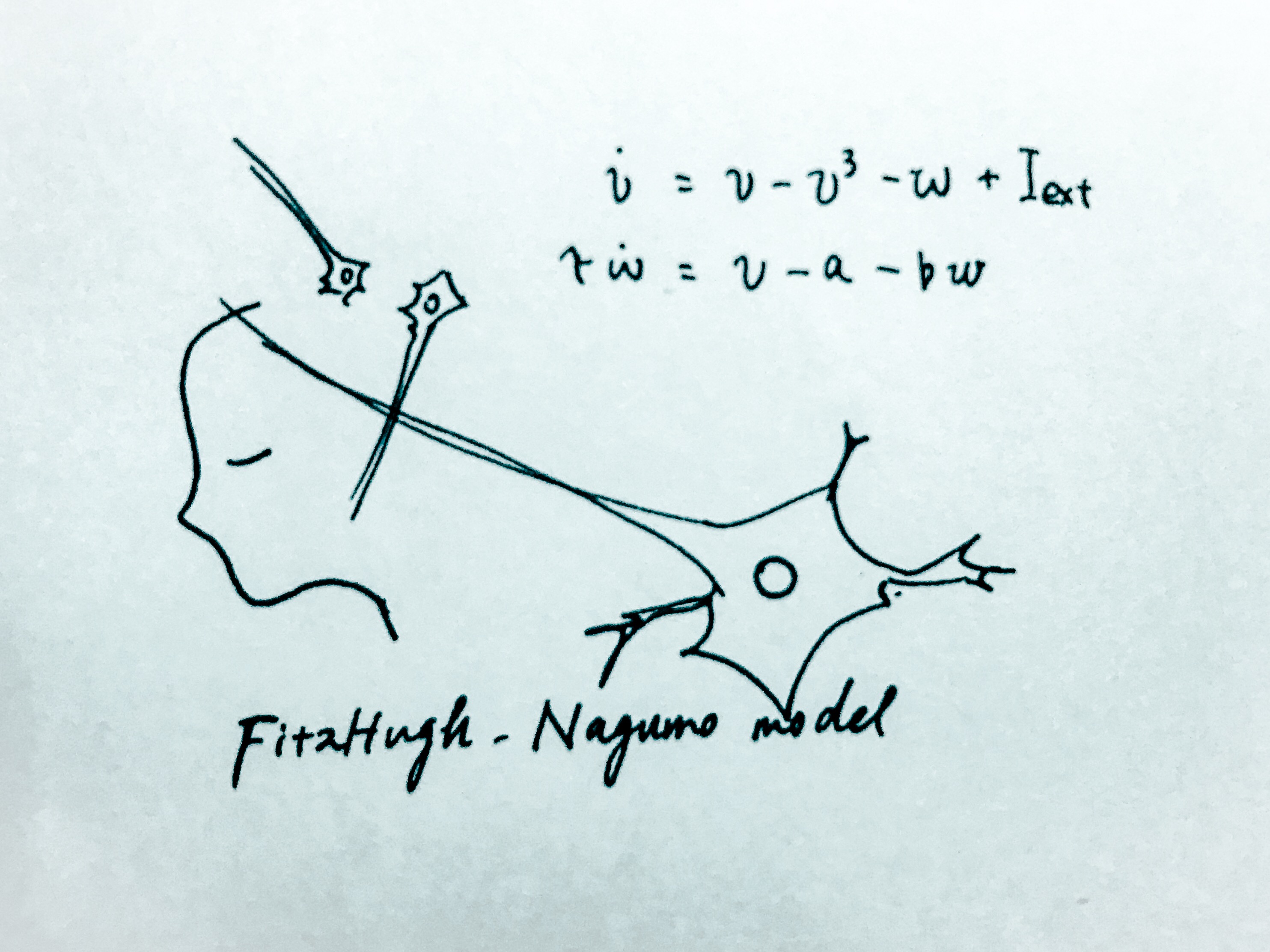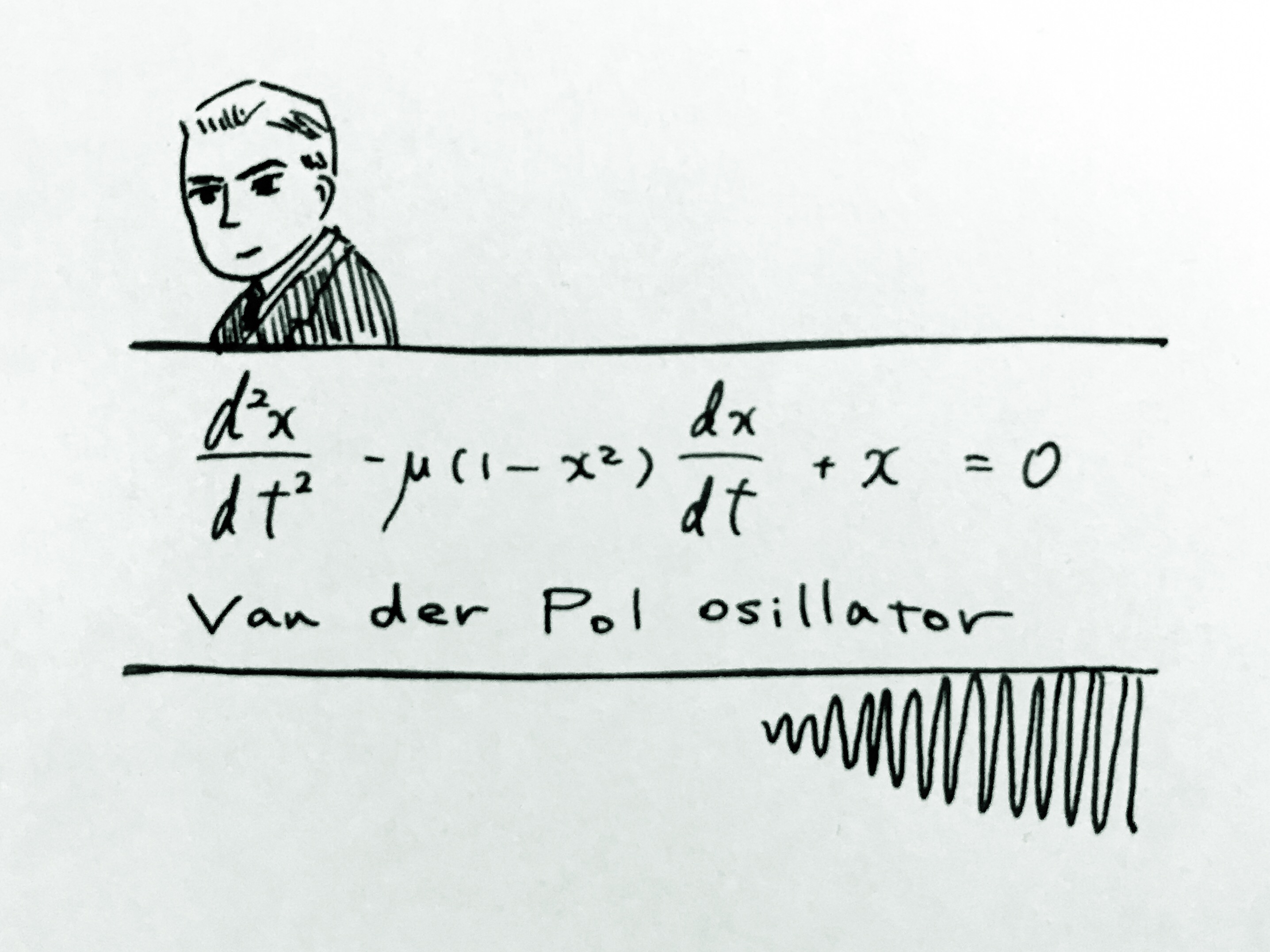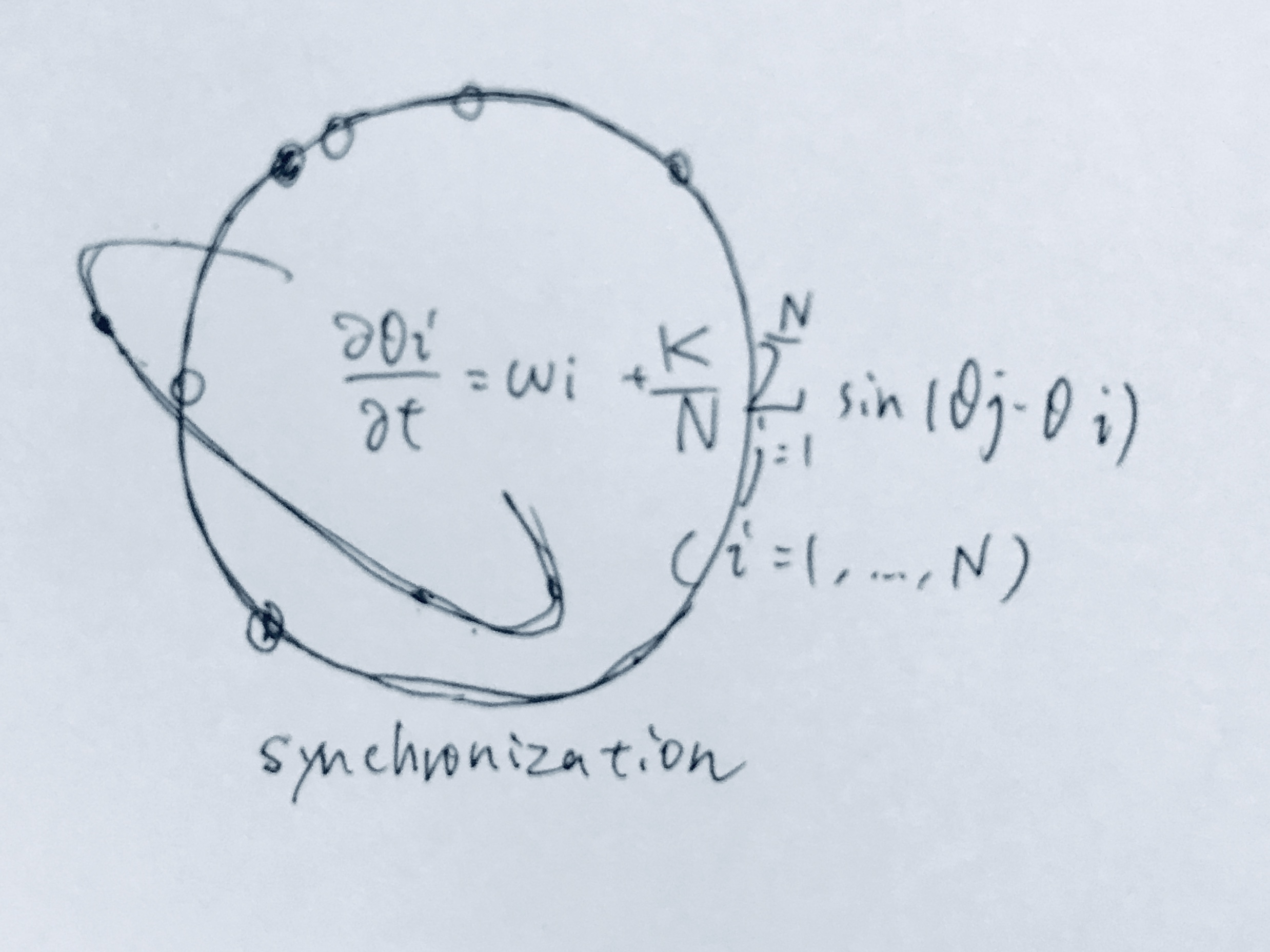
今日の方程式。
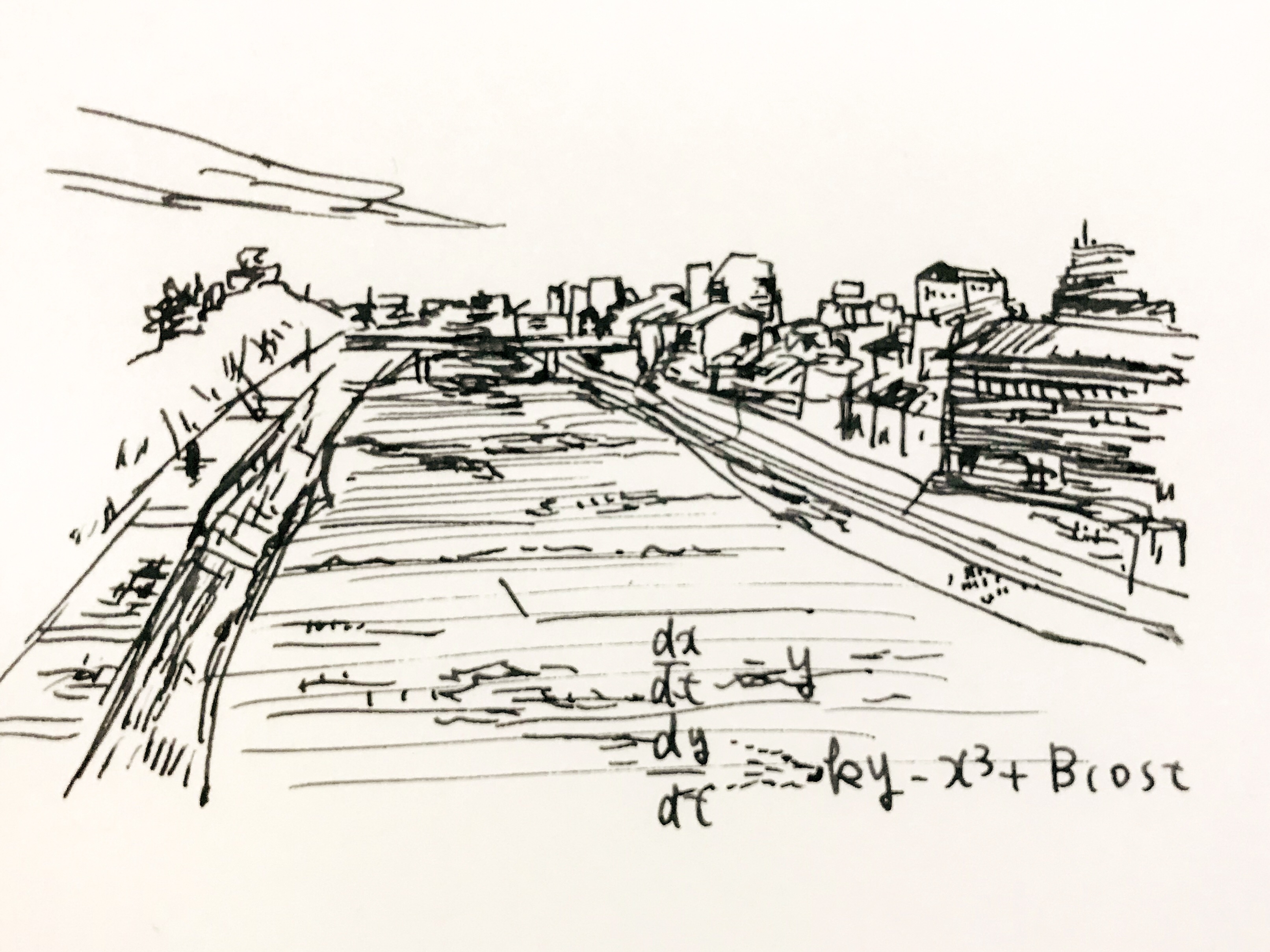
ジャパニーズ・アトラクタを示す
微分方程式。

カオスの先駆的な研究の一つです。

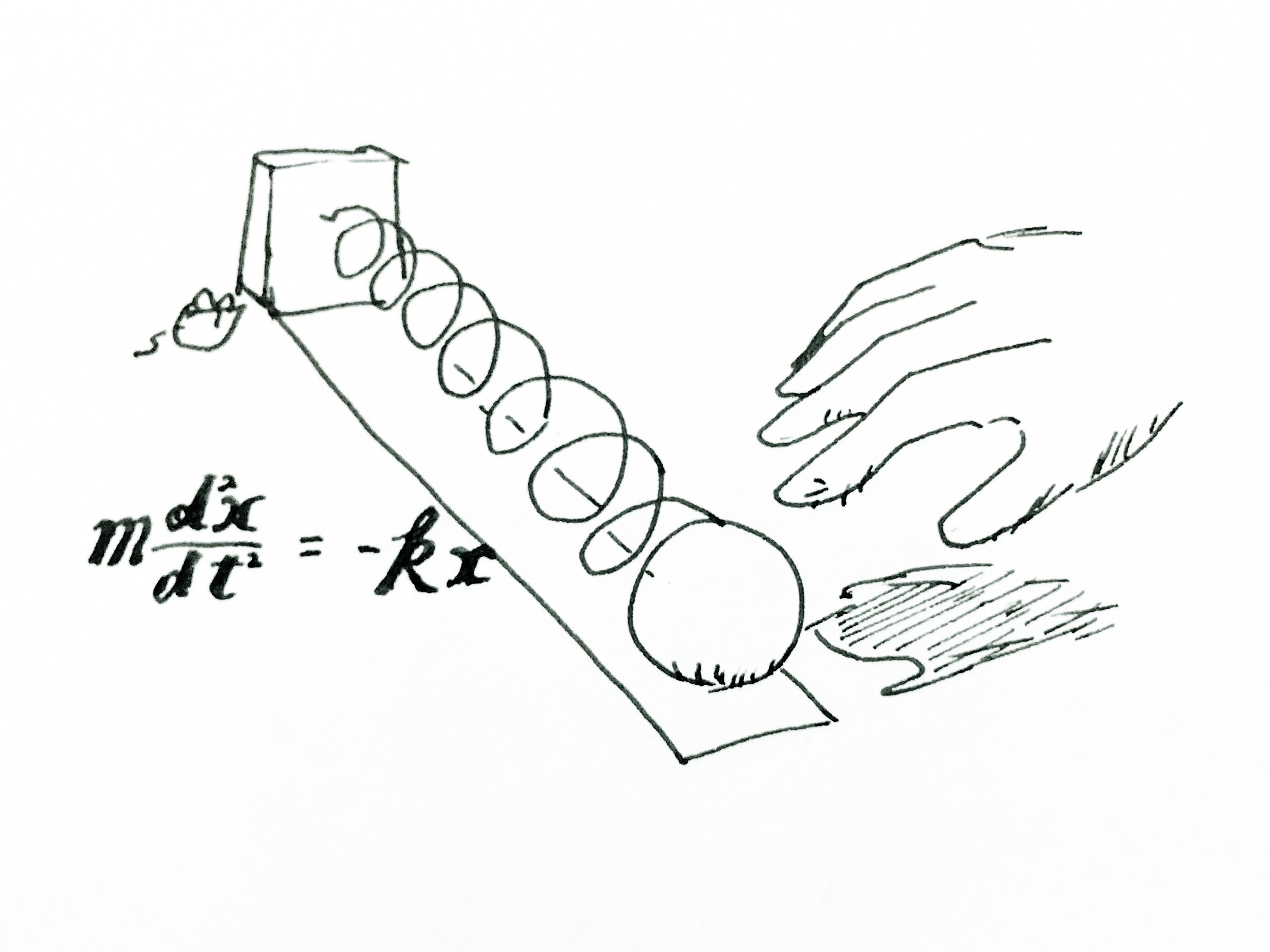
フックの法則に従わない
ばねの運動を再現します。

この方程式を満たすxとyは
カオス軌道を描きます。

これを発見したのは
当時京都大学大学院生だった、
上田睆亮（よしすけ）。
1961年のことでした。
当時はカオスという言葉もなく、
日本国内では注目されませんでした。

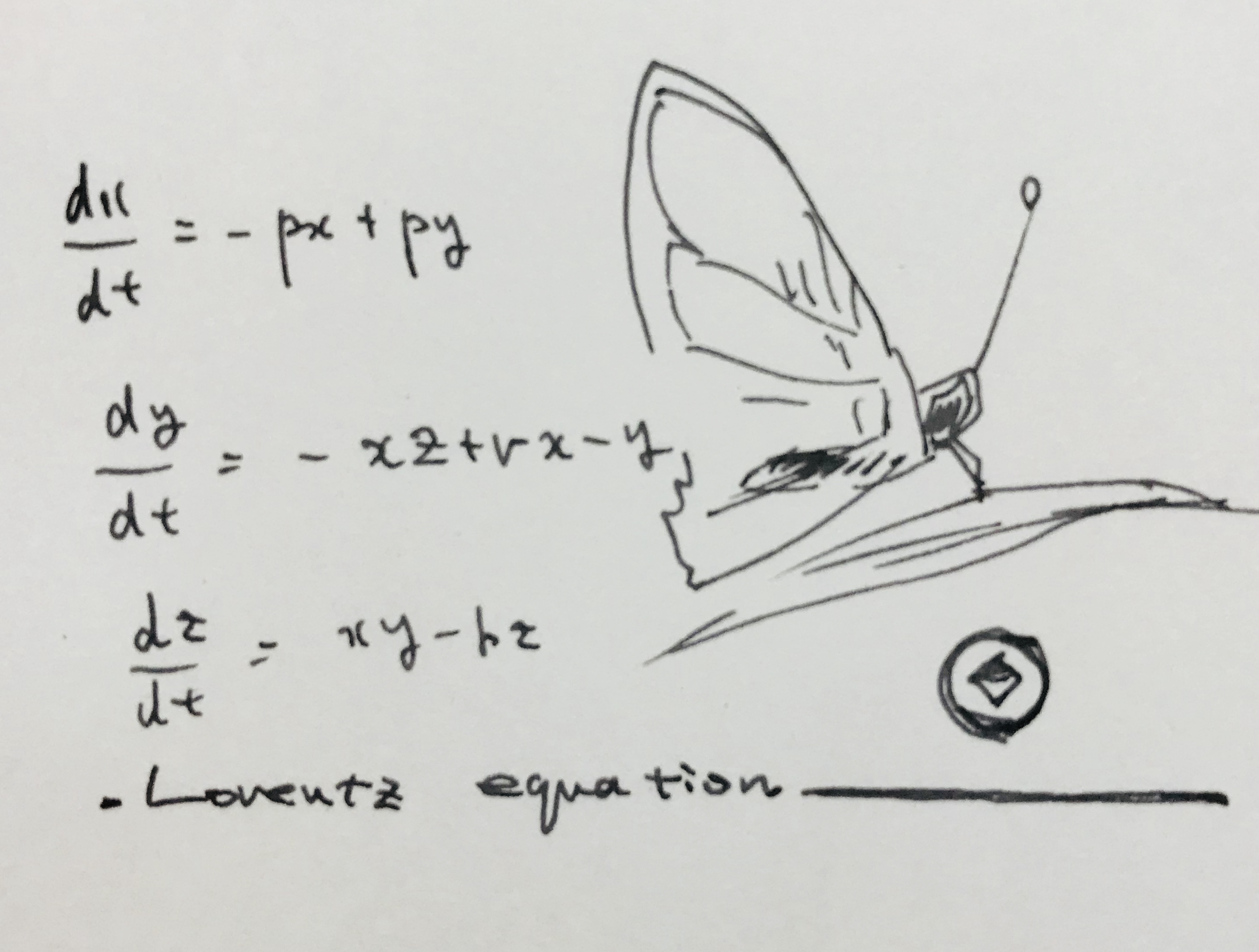
同じくカオスを示す
ローレンツ・アトラクタ―は
1963年の論文で報告されました。

その後上田の発見は1980年の
フランスの数理物理学者による論文で
日の目をみることとなります。

さらに上田は、この発見のまえに
1961年、カオス軌道を示すモデルを
すでに発見しています。

1960年代初めごろは、
世界でも同時多発的に
カオスが発見されていたのですね。

これはコンピューター技術の発展が
深く関わっていそうです。
うーん、どうしても長くなってしまう。
それはまた今度…。

今日の方程式。
水平ばね振り子の運動方程式。

高校で物理を履修したので、
黒板に書いてあったのを思い出します。

このとき小球は、
単振動という往復運動をします。

単振動は「調和振動」ともいい、
数理モデルの中で調和振動をするものを
「調和振動子」といいます。
英語でいうと、”harmonic oscilator”。
なんだかかっこいい。

今日の方程式。
神経細胞のふるまいを再現する、
フィッツヒュー・南雲モデル。

ホジキン・ハクスリーモデルという
モデルをかんたんにしたもので、
生物リズムを表す代表的な方程式です。

この方程式の特殊な場合が、
ファン・デル・ポール方程式。
こちらは真空管を用いた
電気回路についての研究から生まれました。

見た目には異なる現象も、
数理モデルにすることで
現象の核となる部分が取り出され、
同じ核をもつ現象とつながっていきます。

こういうところも、
物理学のおいしいところというか、
おもしろいところだと思います。

こんばんは。かきもちです。

少し前になりましたが、
10月13日、14日に
学生力学系の会という
（平たく言うと）勉強会に
参加してきました！

場所は京都大学。
人生初、関西への単独旅行です。
（関西空港、めっちゃ広かった）

京大付近は、
空気がにやにやしていて
「あー、ここが森見登美彦の…」
と勝手に納得していました。

それはそうとこの会、
力学系という分野を研究する
修士・博士の先輩方が、
学部生向けにプレゼンする、
というもの。

それまで興味をもったことに
「力学系」という言葉が
何度も出てきていたので、

「とりあえず行ってみよう」

と行くことを決意したのでした。

～後編へつづく～

今日の方程式。

真空管の中のカオス、
ファン・デル・ポール振動子。

このモデルを提案したのは
電気工学者、物理学者の
ファン・デル・ポール氏。
1900年代前半、ドイツの
科学者です。

この方程式、
自励振動という運動を
示すモデルのひとつ。

自励振動とは、
外から物体に加わった力が
振動させるような力でなくても、
物体が振動させるような力に変えて
自ら振動してしまう現象のこと。

北リポでは、これを使って
お風呂場見られるお湯の波面を
説明しようとしたことがあります。
（できなかったけど…）

数理モデルは、
いろいろな現象と
つながっていますね。

×　osillator
○　oscillator

今日の方程式。

捕食者ー被捕食者関係を記述する、
ロトカ・ヴォルテラの方程式。

食べられるほうの数が増えると、
食べる方の数が増え、

すると食べられるほうの数が減り、
食べるほうもご飯に困って減る…

その間に食べられるほうが回復し…

という、
食べるほうと食べられるほうの
数の増減を表しています。

ロトカさんとヴォルテラさんが、
二人ともべつべつに考案したモデルです。

いずれも1900年代はじめごろに
考案しています。

 

今日の方程式。

同期現象を記述する、蔵本モデル。
その最もかんたんな場合を表す
方程式です。

リズムをもつものが集まったとき、
それらが相互作用して
リズムが揃えていく様を
表すことができます。

たとえば、ホタルの光。
東南アジアでは、
ひとつの木にとまった蛍が
一斉に明滅するそうです。

たとえば、心臓の拍動。
一つ一つの細胞が
リズムを刻んでいて、
それらのリズムが揃って
全体として拍動しています。

私とあなたも、
相互作用でつながっているのかも。

今日の方程式。

カオスが現れる、ローレンツ方程式。

1963年、E.Lorentzによって
提案された数理モデルです。

紙とペンでその解を求めることはできず、
数値計算によって解を調べます。

このモデルでは、計算の初期値を
ほんの少し変えるだけで、
軌道がまったく変わってしまいます。

予測できない、でもある方程式に従う
不思議な現象、カオス。

その研究の幕開けとなった
記念碑的な方程式です。