最近の研究の相棒を紹介します。
せるおーとまとん君です。
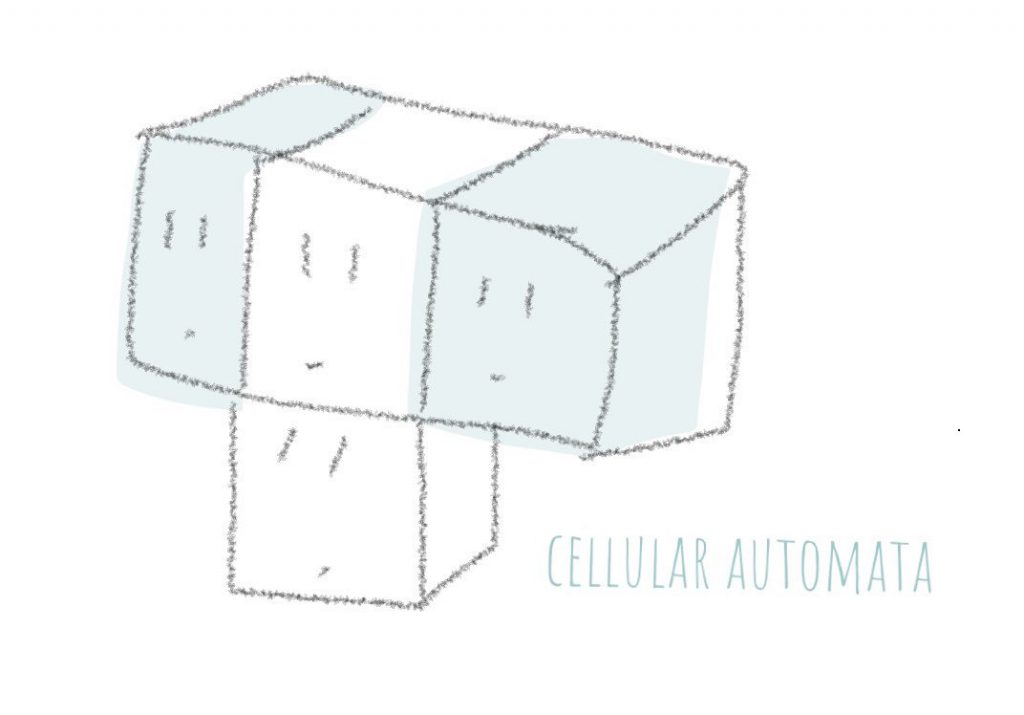
一つ一つの四角が、
周りの様子や自分の様子に合わせて
色を変えます。
絵でいうと、
上1段目の真ん中の四角が
右と左にいる四角の様子を見て
色を変えます。
変わったあとのが、2段目の四角。
(この場合は白のままだけど…)
かわいくておもしろいやつなんです。
またそのうち紹介しますね。
~北国で科学を学ぶ日々~
Photoshopの練習を兼ねて、壁紙を作ってみました。

以下からダウンロードできます。
https://dropbox.com/s/fpk804jxc0d4bxn/kabegami_1.jpg?dl=0…
ご自由にお使いください!
(感想をいただくととても喜びます)
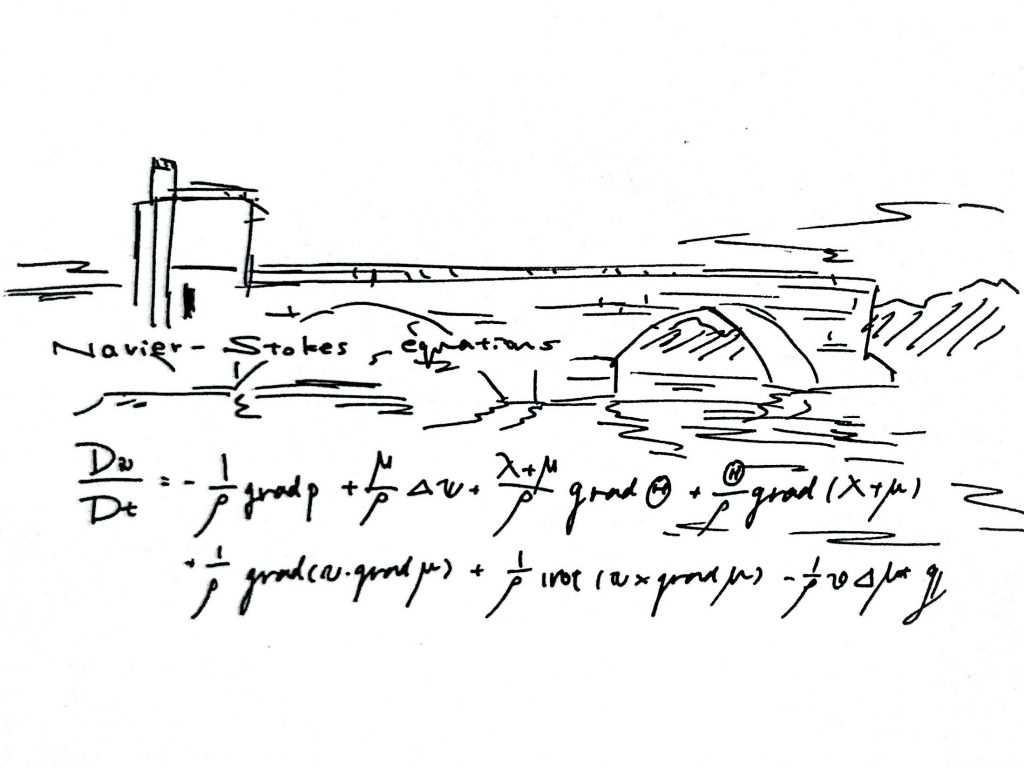
流体力学の基礎方程式。
基礎方程式とは、ニュートン力学でいう
運動方程式に当たるものです。
これを導いたのはアンリ・ナビエ。
19世紀フランスで活躍した、
技術者・科学者です。
この方程式、条件つきの場合を除いて
数学的な厳密解が見つかっていません。
解けるかどうかもわかっていないのです。
人類が流体を掴む日は来るのでしょうか…
REF:
パテント2013 知恵の輪 Vol.24
Wikipedia
予備校のノリで学ぶ ナビエ-ストークス方程式
ホーストン大学 Engines of Our Ingenuity
https://uh.edu/engines/epi2832.htm
最近、「今日の方程式」を
更新していて思う。
科学のことを正確に、
楽しく伝えるのって
難しい…。
勉強がまだ生焼けなので、
自分が思っている
おもしろポイントが
勘違いということがあるのだ。
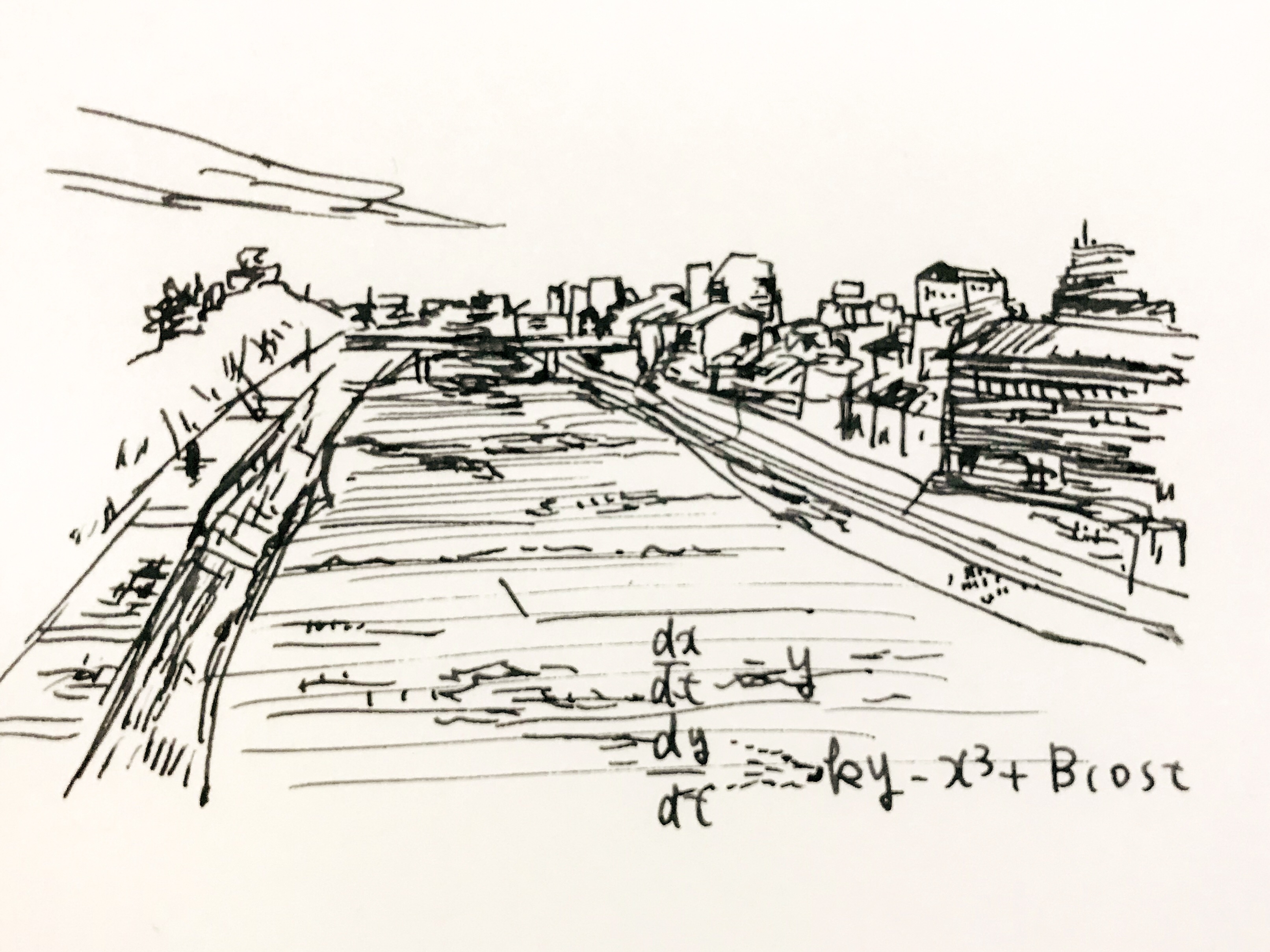
今日の方程式。
ジャパニーズ・アトラクタを示す
微分方程式。
カオスの先駆的な研究の一つです。
フックの法則に従わない
ばねの運動を再現します。
この方程式を満たすxとyは
カオス軌道を描きます。
これを発見したのは
当時京都大学大学院生だった、
上田睆亮(よしすけ)。
1961年のことでした。
当時はカオスという言葉もなく、
日本国内では注目されませんでした。
同じくカオスを示す
ローレンツ・アトラクタ―は
1963年の論文で報告されました。
その後上田の発見は1980年の
フランスの数理物理学者による論文で
日の目をみることとなります。
さらに上田は、この発見のまえに
1961年、カオス軌道を示すモデルを
すでに発見しています。
1960年代初めごろは、
世界でも同時多発的に
カオスが発見されていたのですね。
これはコンピューター技術の発展が
深く関わっていそうです。
うーん、どうしても長くなってしまう。
それはまた今度…。
今日の方程式。
真空管の中のカオス、
ファン・デル・ポール振動子。
このモデルを提案したのは
電気工学者、物理学者の
ファン・デル・ポール氏。
1900年代前半、ドイツの
科学者です。
この方程式、
自励振動という運動を
示すモデルのひとつ。
自励振動とは、
外から物体に加わった力が
振動させるような力でなくても、
物体が振動させるような力に変えて
自ら振動してしまう現象のこと。
北リポでは、これを使って
お風呂場見られるお湯の波面を
説明しようとしたことがあります。
(できなかったけど…)
数理モデルは、
いろいろな現象と
つながっていますね。
× osillator
○ oscillator