最近寒さが厳しいですね。
札幌は最高気温が氷点下になり、
昼間ならあったかいし…！という希望も
少し薄れています。つらい。つららら。
あんまり寒いので、春の使徒が見たくて
ミュシャを検索して描いておりました。
（『四季』を参考に描きました）
目の前にあるものよりも、ないもののほうが
くっきりとした輪郭で掴めることって
あるんですね。
今、私にとっては、
春の姿というのがそれです。
（要はあたたかくなってほしい）
（ほんとに寒い）
No.306「大学4年目1月」
お久しぶりです。かきもちです。
あれ、前の投稿からそんなに経っていないのか…
この1週間は長く感じたなあ…
久々に4コマ、近況報告を書きました。
おかげさまで元気にやっております。
No.305「受け身をとる」
かきもちです。
あけましておめでとうございます。
昨年はお世話になりました。
今年もよろしくお願いします。
ちょっと昨年がんばりすぎたので、
ここらで一息落ち着いて、
日常に戻る準備をしたいと思います。
札幌通信ー11月号
10月もはやかったですが、
11月もすごいスピードで
過ぎていきました…！
もはや年末感すらある。
こういうときは過度に過去を
まとめようとするので、
危ないです…！（精神衛生上）
ともあれ、いろいろありました。
No.304「発信についての考察」
No.303「科学を伝える難しさ」
最近、「今日の方程式」を
更新していて思う。
科学のことを正確に、
楽しく伝えるのって
難しい…。
勉強がまだ生焼けなので、
自分が思っている
おもしろポイントが
勘違いということがあるのだ。
No.302「ねずみ図解」
No.301「おえかきするわけ」
No.300「ジャパニーズ・アトラクタ」
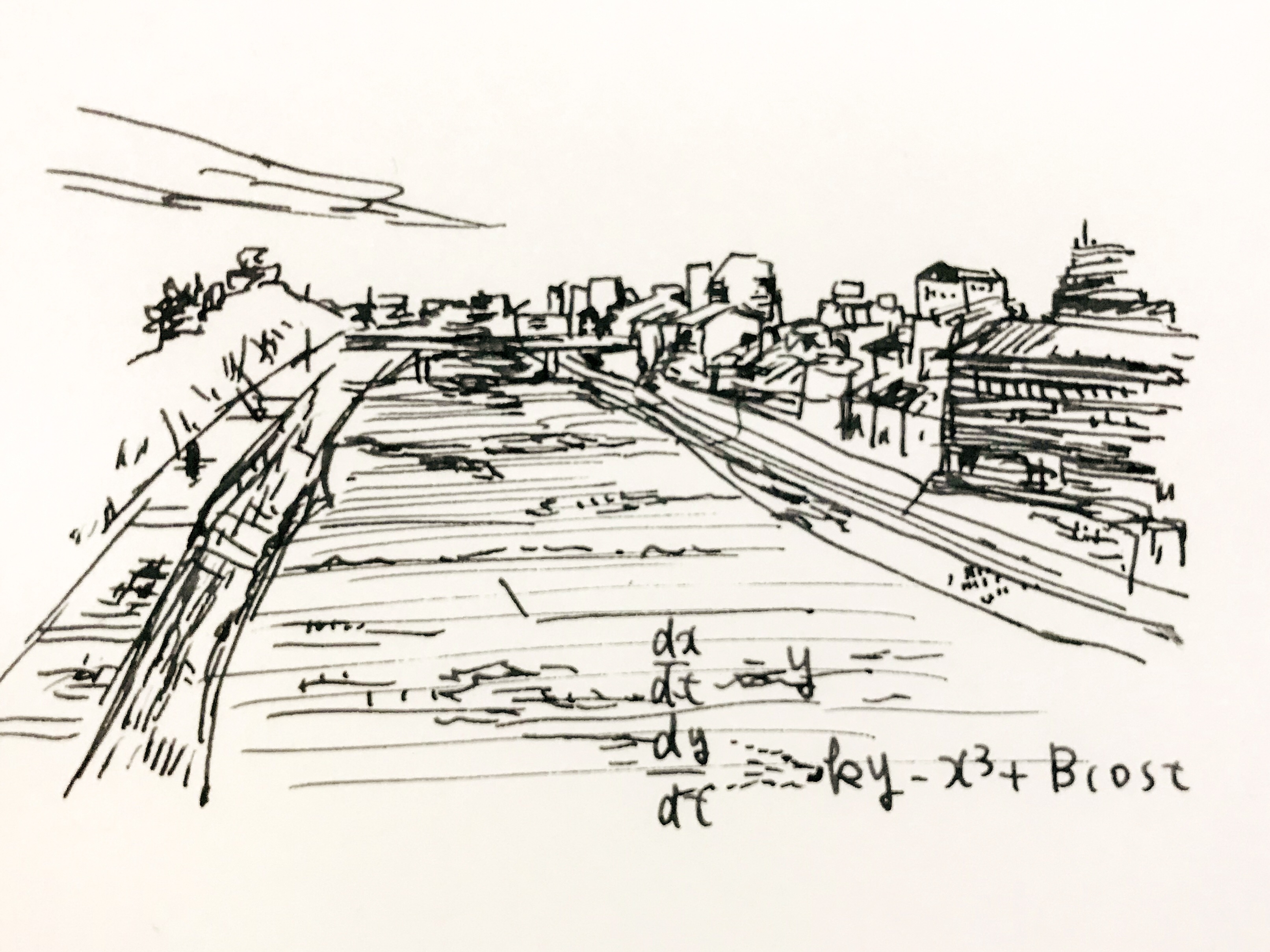
今日の方程式。
ジャパニーズ・アトラクタを示す
微分方程式。
カオスの先駆的な研究の一つです。
フックの法則に従わない
ばねの運動を再現します。
この方程式を満たすxとyは
カオス軌道を描きます。
これを発見したのは
当時京都大学大学院生だった、
上田睆亮（よしすけ）。
1961年のことでした。
当時はカオスという言葉もなく、
日本国内では注目されませんでした。
同じくカオスを示す
ローレンツ・アトラクタ―は
1963年の論文で報告されました。
その後上田の発見は1980年の
フランスの数理物理学者による論文で
日の目をみることとなります。
さらに上田は、この発見のまえに
1961年、カオス軌道を示すモデルを
すでに発見しています。
1960年代初めごろは、
世界でも同時多発的に
カオスが発見されていたのですね。
これはコンピューター技術の発展が
深く関わっていそうです。
うーん、どうしても長くなってしまう。
それはまた今度…。
